OBJECTIVE: I will be able to calculate the equivalent resistance when more than one resistor is present in an electrical circuit after today's class.

I will be able to calculate the equivalent capacitance when more than one capacitor is present in an electrical circuit after today's class.

TERMS:

• Capacitor - two charged surfaces that can store electrical energy
• Resistor - an object in an electric circuit which interferes with the flow of electrons through that circuit.
• Series: occurs when items in a circuit are connected in a line
• Parallel: occurs when items in a circuit
• ElectroMotive Force = EMF= ε=Voltage

UNITS:

• Capacitance = C
  • (SI Units "farads" = f)
• EMF = ε =Voltage generated inside a battery
  • (SI Units = "Voltage or Volts"="V")
• Voltage = ∆V = Voltage available to a circuit
  • (SI Units = "Voltage or Volts"="V")
• Current = I = Current through an electrical circuit
  • (SI Units = "amperes or Amps"="A")
• Ohms = R=resistance =
  • (SI Units = "ohms" = Ω)
• Power = P = I²R
  • (SI Units = "Watts" = W)

FORMULAE:

• ε=IR (ε = ElectroMotive Force) = Total *oomph* inside the battery, it is not generally equal to the voltage output by the battery because of the internal resistance inside the battery
• ∆V = IR = "Ohm's Law": (We'll use this UNLESS EMF is given)
• P = I²R = Power

WORK O' THE DAY: 

Let's take a few moments to make sure we're acquainted with ALL the componants of an electrical circuit we'll be working with over the next few days (see above).

Notice that we describe each componant one way:

voltage (V), capacitance (C), current (I), resistance (R), Power (P) but we (mostly) use different values for the actual units of those when we are doing circuit analysis and/or calculations with varrying uppercase/lowercase and Greek letter conventions:

voltage (Volts), capacitance (farads), current (Amps), resistance (Ωhms), Power (Watts) but we (mostly) use different values for the actual units of those when we are doing circuit analysis and/or calculations

Take a few moments to quiz each other to make sure we have a good start with those

════════════════════

We had a request for me to provide my AP type problems for you... that prompted me to come up with THIS.

Let's discuss

════════════════════

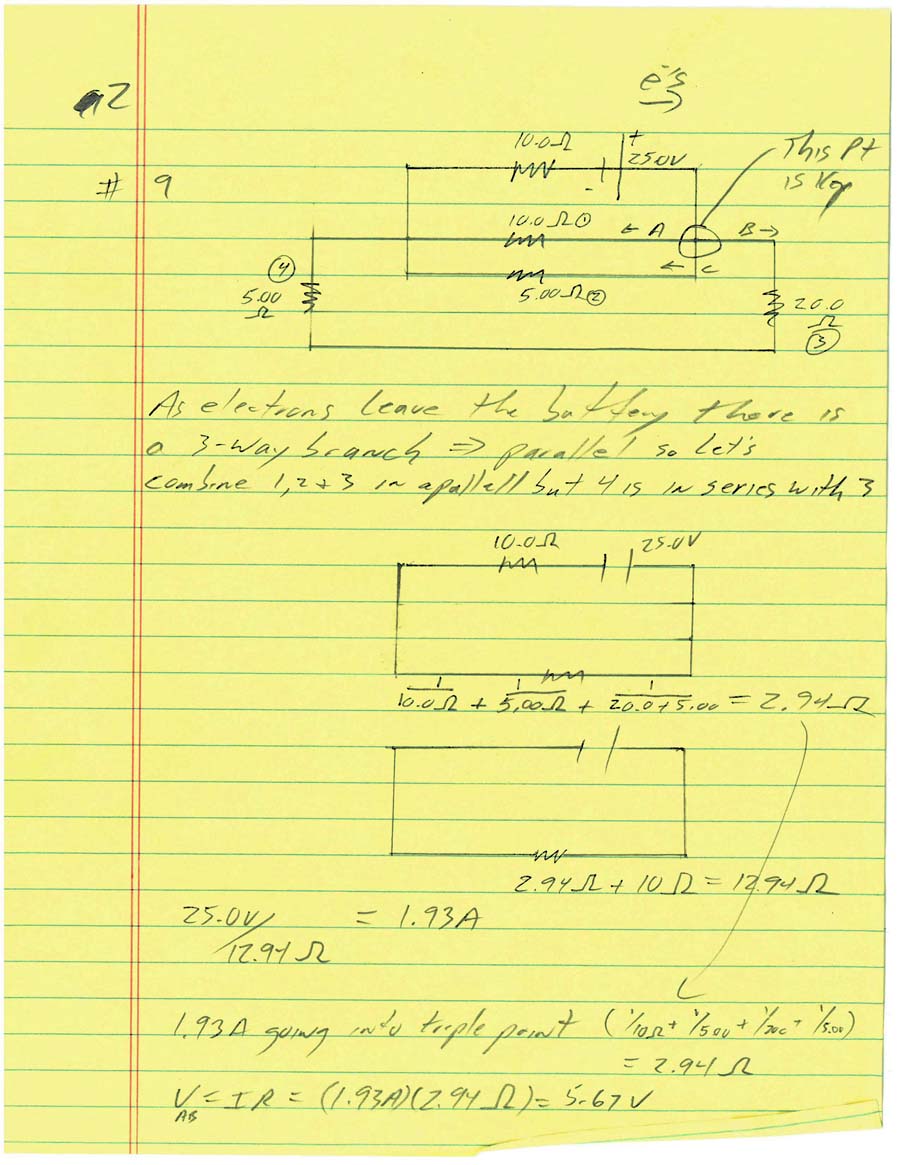
Recollect to your group, if you would please, the rules for determining capacitance for capacitors in series and in parallel...

The sorta good news is that is ALMOST the same for resistors in a circuit.... 'cept backwards.

 

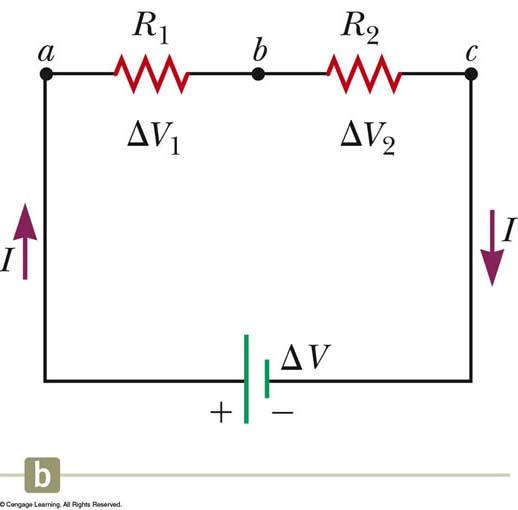
Here's an example of a simple circuit showing two resistors in series:

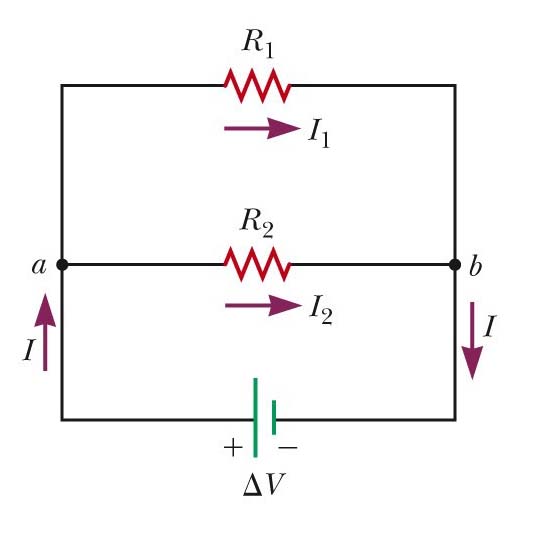
The following image shows two resistors in parallel:

Circuit rule #1: We add resistors when they are in series and we add their reciprocals when they are in parallel (note: we use the subscript "eq" to denote "equivalence"... you can think of that as "total" and be just fine)

Adding resistors in series:

R_eq = R₁ + R₂ + R₃ etc....

Adding resistors in parallel:

 

1/R_eq = 1/R₁ + 1/R₂ + 1/R₃ etc....

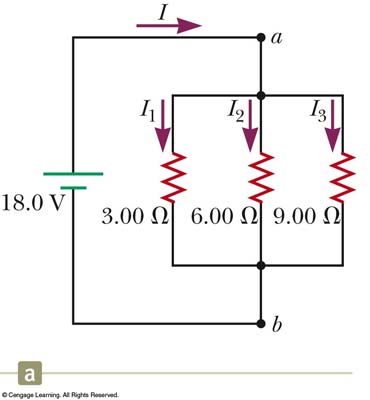
For example:

 

.

We can (and should) think of those 3 resistors in parallel as a single resistor with resistance:

1/R_eq =1/3.00 + 1/6.00 + 1/9.00 = 1.63Ω

Notice that we can now find the TOTAL current through the circuit using Ohm's Law thusly:

∆V=I_TotR_Tot

∆V/R_Tot=I_Tot

18.0V/1.63Ω = 11.1 A

Not surprisingly (I hope) we can find the current through EACH resistor too:

V = I₁R₁

V/R₁= I₁

18.0V/3.00Ω = 6.00A

V = I₂R₂

V/R₂= I₂

18.0V/6.00Ω = 3.00A

V = I₃R₃

V/R₃= I₃

18.0V/9.00Ω = 2.00A

I_Total = I₁+I₂+I₃ = 11A YAY!!!

Which is to say the current going in gotta equal the current going out! or more officially:

The current going into a junction is equal to the current coming out of the junction!

Things will get a tad bit dicier in the next section when we apply more (Kirchoff!) rules!

════════════════════

Work through examples 28.6, 8, 9 & 17 begining on page 858 ... those should be pretty straightforward.

════════════════════

ANSWERS: